RL for Training Multiple Decoding Heads -- An Inference Acceleration Method in Language Models (ICLR 2025 Workshop on Sparsity in LLMs)

Medusa Inspiration

I recently read the Medusa paper from Together AI and it scratched an itch that I had been wondering about for a while. For fully deterministic LMs (pure logit argmax for token selection), given tokens \(t_0,t_1\dots t_n\), we can represent the next token to be generated as the output of a function \(t_{n+1}=f(t_{1:n})\). However, if \(t_{n+1}\) is fully determined by \(t_{1:n}\) and no arbitrary random variable \(X\)(attributed to stochasticity in token sampling with certain LM inference techniques), then if \(t_{n+2}=f(t_{1:n+1})\), since \(t_{n+1}\) is purely a function of the first \(n\) tokens, there exists a reparametrization of the function where \(t_{n+2}=g(t_{1:n})\). This is definitely a function that we can learn, effectively taking a “next token predictor” and expanding it to a “\(k\) tokens in advance predictor”.

The Medusa paper essentially focuses on this technique. Given a base LM \(g_1\) that predicts the next token given some context \(t_{1:n}\), can we LoRA finetune \(k-1\) instances of this base LM \(g_2,g_3\dots g_{k}\) such that \(g_i\), given context \(t_{1:n}\) predicts token \(t_{n+k}\)? Then by calling all \(k\) of these models in parallel we can generate \(k\) tokens at a time instead of \(1\). This technique gained significant popularity and is now included in many awesome packages like vllm and TensorRT-LLM.

An RL Approach

We propose an RL approach to train a second decoding model that predicts token \(n+2\) based on the context of tokens \(t_{1:n}\). We initialize this second model to the base GPT-2 weights and split the reinforcement learning teaching process into two steps:

1. Reward Model Fitting: We train a reward model to take in the last hidden state of the context input as well as a token embedding, that outputs a probability representing how likely the token corresponding to the inputted embedding will be the \(n+2\)-nd token given the last hidden state (representing the final hidden state of the \(n\)-th token, which should be a representation-rich vector of the whole context). We can assume that the last hidden state(call this \(h_n\)) represents the state in a traditional RL interpretation, and the token embedding represents the action in an RL interpretation, as it is the proposed \(n+2\)-nd token. Given an accurate reward model, then maximizing the reward would mean selecting tokens that have the highest probability of being the \(n+2\)-nd token given the context of the first \(n\) tokens (hidden state). To train this, we sample trajectories from the initial base GPT(next token predictor) of 20 tokens sampled per trajectory using a wikipedia dataset from the datasets library. Then, for each generation step \(t\), we sample a set of 9 token candidates to fit the reward model on: 1 is the highest probability token, 3 from the top 50 probability tokens, and 5 random tokens. This is done to ensure that the reward model is trained on a sufficient variety of token types and compute constraints prevent us from training on all token candidates at each step, as the reward model is fitted on a Apple M3 Chip.

To formalize this method, for a given trajectory, if we have \(j\) tokens of context of starter tokens from our wikipedia context. Then, we can train our reward model based on tokens \(j+2,j+3\dots j+20\). For token position \(j+i\), we can find a probability vector \(p_{j+i}\) for the appropriate tokens. We sample 9 of these tokens using the described scheme and fit the reward model so that given the context of the first \(j+i-2\) tokens (final hidden state of token \(j+i-2\)), then we fit the model to take in this hidden state as well of the token embedding of each of these 9 tokens and predict its probability well. We make this reward model as a simple FFNN trained with a MSE Loss. Here’s a plot of the MSE Loss. Note that for each step’s loss, we aggregate the loss for each of the 9 token candidates, 19 considered steps, and 15 trajectories before running backprop. So, each loss step can be interpreted as an aggregation of \(9*19*15\) (trajectory,step,token candidate) tuples.

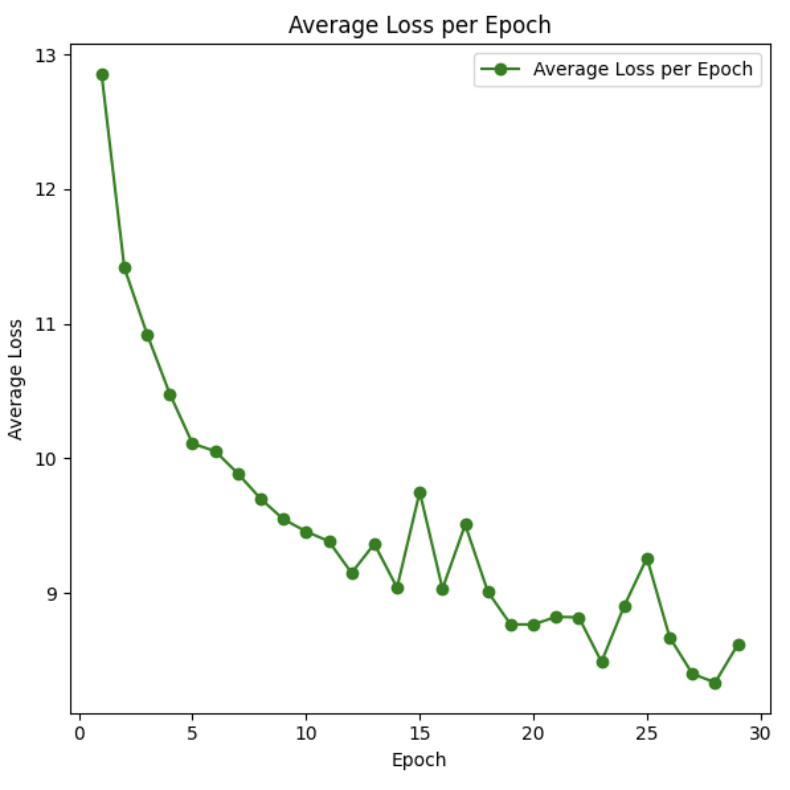
Next steps to make this production-grade would be using a more powerful model and running this for some more epochs. Note that in the above graph the first epoch was eschewed as it had an average loss of around 50 in order to visually show the learning progress of other epochs better.

1. Train new decoding model: Given a robust reward model, we want to use it to tune an instance of the base gpt 2 model so it can accurately predict 2 tokens in advance. We do this with PPO, where we want to maximize the reward function minus a KL term(\(r-\beta KL(m_1,m_2)\)), with the KL term representing the distance from our tuned gpt 2 instance and the original base instance to ensure that any characteristics exploited to maximize the expected reward don’t take away from it’s nature as a language model that should have reasonable outputs. For each step, treating our GPT 2 instance as a policy we want it to choose actions (i.e. token selections) that have maximal probability of appearing 2 tokens in advance when simulating from the base GPT. With this interpretation, we train our decoding head to take in the context of the first \(n\) tokens in some prompt and sample the projected token that will occur as the \(n+2\)-th token with a reasonable degree of accuracy. We train this PPO objective with gradient descent.

By following these steps, we aim to create a robust RL-based decoding model that can predict multiple tokens in advance, enhancing inference speed and efficiency. Here is a how this reward (total reward including KL term) learned over time:

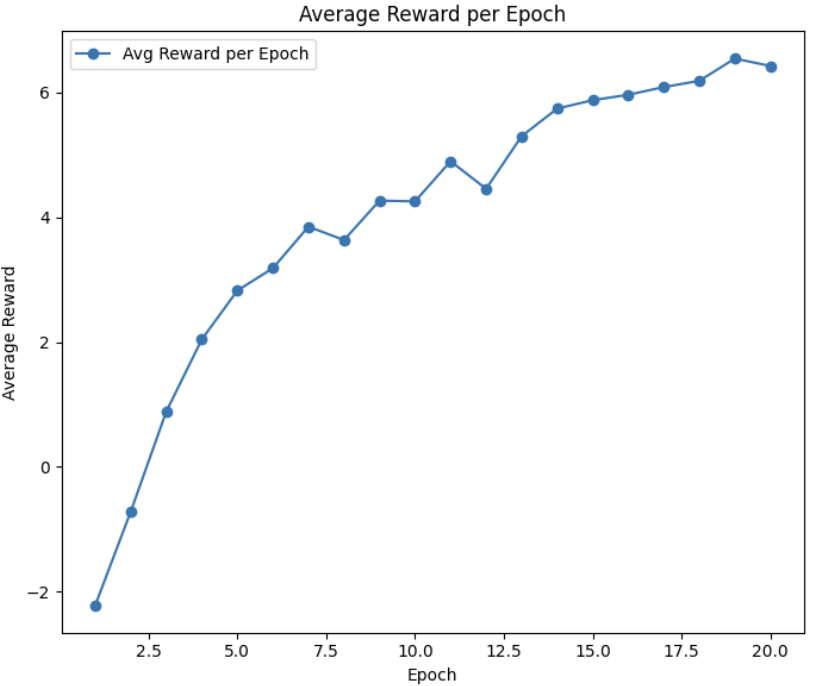
This was trained for 20 epochs on a A100 GPU via Modal Labs.

Inference

So, now we can use our GPT 2 model to predict 1 token in advance and this new model trained to predict 2 tokens in advance? We simply just run both models concurrently, and when get both token results, append both to our context and keep running until we hit an <EOS> token.

Conclusion

Given the compute constraints of this project, I’d love to run this on Llama 8B to see if more exciting performance benefits can be realized. Check out the github or email me if you want to talk about this project or suggest some changes!